Chemical formulae and Equations
A chemical formula consist of a symbol or symbols showing the number of atoms in one molecule of an element or a compound
Steps to consider when writing the chemical formula
- Write the symbol for the combining elements and radicals
- Write the Valency of each element or radical at the top at its top right hand side
- Exchange the Valencies of the combining elements and radicals by writing them at the bottom right hand side of the element or radical. If the number is 1, do not write it.
In some formulae, radicals are written in brackets followed by a small sub script digit.
Example 1
Write the formula for each of the following compounds
(a) Sodium chloride
(b) Potassium carbonate
Solution
(a) Na Cl
=
Answer: NaCl
(b) K
=
Answer:
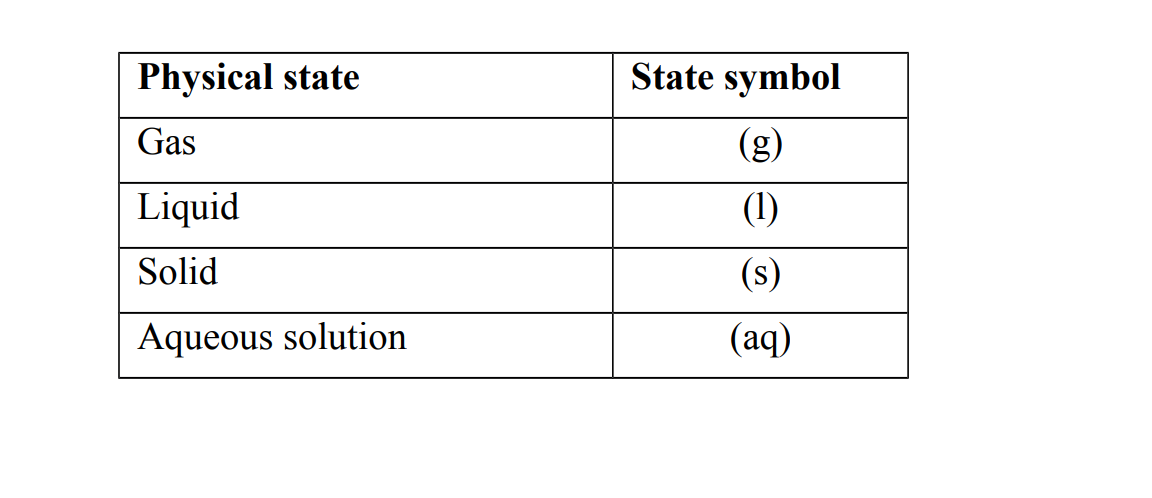
State symbols
State symbols are letters that are used to show the physical state of substances in the equation State symbols are placed in brackets after the name or formula of each substance in the equation
Equations
An equation is a chemical sentence which describes what is happening in a chemical reaction
An equation can be represented in the form:
A + B → C + D
The plus (+) sign on the left hand side means “react with”
The plus (+) sign on the right hand side means “and”
The arrow (→) between the reactants and products means “to form”
Word equations
Word equations are chemical equations written in words
Example 2
Write down the word equation for each of the following reactions including state symbols
(a) Magnesium metal reacts with oxygen gas to form magnesium oxide
(b) Hydrogen sulphide gas reacts with oxygen gas to form sulphur and water
(c) Iron (II) chloride solution and hydrogen gas are produced when iron reacts with dilute hydrochloric acid
(d) Iron reacts with chlorine gas to form iron (II) chloride
Solution
(a) Magnesium(s) + Oxygen(g) → Magnesium oxide(s)
(b) Hydrogen sulphide(s) + Oxygen(g) → Sulphur(s) + Water(l)
(c) Iron(s) + Hydrochloric acid(aq) → Iron (II) chloride(aq) + Hydrogen(g)
(d) Iron(s) + Chlorine(g) → Iron (II) chloride(s)
Equations with symbols
Writing balanced chemical equations
Balancing the equation is the process of making the number of each type atom equal on both sides of the equation
Example 3
Write down balanced chemical equations including state symbols for each of the following word equations
(a) Mercury oxide(s) → Mercury(l) + Oxygen(g)
(b) Hydrogen(g) + Oxygen(g) → Water(l)
(c) Magnesium(s) + Oxygen(g) → Magnesium oxide(s)
(d) Sodium(s) + Water(l) → Sodium hydroxide(aq) + Hydrogen(g)
(e) Calcium oxide(s) + Hydrochloric acid(aq) → Calcium chloride(aq) + Water(l)
Solution
(a) 2HgO(s) → 2Hg(l) + (g)
(b) (g) + (g) → (l)
(c) (s) + (g) → (s)
(d) (s) + (l) → (aq) + (g)
(e) (s) + (aq) → (aq) + (l)
Ionic equations
Ionic equations show only the ions involved in a chemical reaction
Ions not taking part in the reaction (spectator ions) are cancelled out in the construction of ionic equations
Steps to consider when writing the ionic equation
- Construct a balanced chemical equation
- Split only soluble ionic compounds into ions. Insoluble ionic compounds, elements and covalent compounds remain unchanged.
- Cancel out spectator ions. These are ions that appear on both the left and right hand side of the equation.
- Rewrite the equation without the spectator ions
Example 4
Write the ionic equations for the reactions below
(a) (aq) + (aq) → (s) + (aq)
(b) (aq) + (aq) → (aq) + (l)
Solution
(a) (aq) + (aq) → (s) + (aq)
= (aq) + (aq) + (aq) + (aq) → (s) + (aq) + (aq)
Cancel the spectator ions or the same ions in the equation
Answer: (aq) + (aq) → (s) +
(b) (aq) + (aq) → (aq) + (l)
= (aq) + (aq) + (aq) + (aq) → (aq) + (aq) (l)
From the above equation Cancel the spectator ions or the same ions in the equation
Answer: (aq) + (aq) → (l)
Stoichiometric calculations
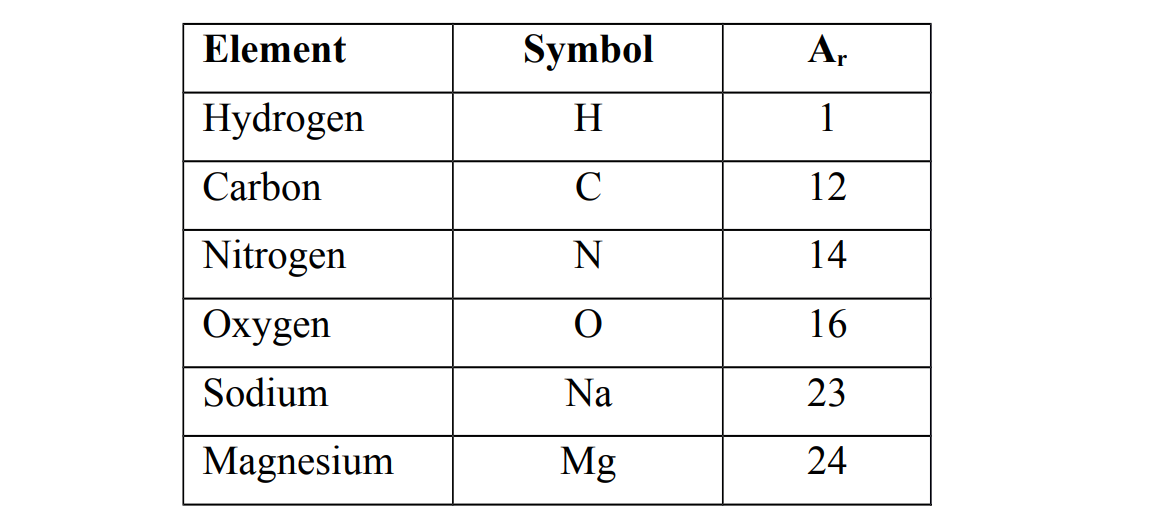
Relative atomic mass
Symbol:
Units: It has no units
Relative atomic mass of an element is the mass of one atom of an element compared to 1/12 the mass of carbon−12isotope.
Relative atomic masses of some elements
Relative molecular mass
Symbol:
Units: It has no units
Relative molecular mass of a compound is the mass of one molecule of the compound or element compared with 1/12 the mass of carbon−12isotope
Relative molecular mass can also be defined as the sum of relative atomic masses
Example 5
Find the relative molecular, , of the following:
(a) Hydrogen chloride, HCl
(b) Carbon dioxide,
(c) Sodium sulphate,
(d) Copper (II) sulphate -5-water, CuSO4.5H2O
Solution
(a) of HCl = (1 x 1) + (1 x 35.5)
= 1 + 35.5
Answer: 36.5
(b) of = (1 x 12) + (2 x 16)
= 12 + 32
Answer: 44
(c) of = (2 x 23) + (1 x 32) + (4 x 16)
46 + 32 + 64
Answer: 142
(d) of = (1 x 64) + (1 x 32) + (4 x 16) + (10 x 1) + (5 x 16)
= 64 + 32 + 64 + 10 + 80
Answer: 250
Molar mass
Molar mass is the mass of one mole of a substance
Symbol: MM
SI unit: gram per mole, g/mol
Molar mass can also be defined as relative molecular mass expressed in grams per mole
Example 6
1 mole of potassium (K), MM = (1x39) = 39g/mol
1 mole of sodium (Na), MM = (1x23) = 23g/mol
1 mole of carbon dioxide MM = [(1x12) + (2x16)] = 44g/mol
Mole
The mole is the amount of substance which contains as many elementary entities as they are in 12.00g of carbon-12 isotope
How to calculating number of moles
n = mole [mol]
m = mass [g]
MM = molar mass [g/mol]
Example 7
(a) How many moles of potassium are there in 3.9g of potassium?
Solution
n = ?, m = 3.9g, MM = 39g/mol
Answer:
(b) Find the mass of 0.2moles of ammonia molecules, .
Solution
n = 0.2 mol, m = ? , MM = 17g/mol
Answer:
(c) How many moles of hydrogen atoms does 3.2g of methane, contains
Solution
MM for = (1 x 12) + (4 x 1) = 16g/mol
n = ? , m = 3.2g, MM = 16g/mol
Number of moles of hydrogen in = number of hydrogen atoms in
= 4 x 0.2mol
Answer: 0.8mol
Avogadro’s number
Avogadro’s number is the number of particles in exactly one mole of a pure substance 12.00g of carbon contains as many as atoms
Alternative term: Avogadro’s constant
Symbol:
1 mole of any element has mass equivalent to its mass number and contains particles.
Example 8
1 mole of Ca = 40g = particles
1 mole of Fe = 56g = particles
1 mole of Mg = 24g = particles
Elementary entities include atoms, molecules, ions, electrons, protons and neutrons
1 mole of atoms = atoms
1 mole of molecules = molecules
1 mole of ions = ions
1 mole of electrons = electrons
1 mole of protons = protons
1 mole of neutrons = neutrons
Example 9
(a) How many atoms of iron (Fe) are there in 25g of iron?
Solution
56g is the mass number of iron
56g → atoms
25g → x
cross multiply to find the answer
Answer: Atoms
(b) What is the mass of atoms of calcium?
Solution
40g is the mass number of calcium
40g → atoms
x → atoms
cross multiply to find the answer
Answer:
Mole to mole calculations
Example 10
(a) How many moles of chlorine are required to react 2.5 moles of calcium to produce calcium chloride?
Solution
1 mol Ca → 1 mol
2.5mol Ca → x
cross multiply to find the answer
Answer:
(b) How many moles of carbon dioxide () will be produced by complete combustion of 2 moles of glucose ( ) according to the equation?
Solution
1 mol → 6 mol
2 mol → x
cross multiply to find the answer
Answer:
Mole to mass calculations
Example 11
(a) What mass of hydrogen can be produced by reacting 6 moles of aluminium with hydrochloric acid?
Solution
2 mol → 6g
6 mol Al → x
cross multiply to find the answer
Answer:
(b) How many grams of oxygen are required to react with 0.3 moles of aluminium to produce aluminium oxide?
Solution
4 mol Al → 96g
0.3 mol Al → x
cross multiply to find the answer
Answer:
Mass to mass calculation
Example 12
(a) Calculate the mass of calcium chloride produced when 40g of calcium carbonate reacts with hydrochloric acid
Solution
100g → 111g
40g → x
cross multiply to find the answer
Answer:
(b) How many tonnes of uranium can be produced in the above reaction using 24 tonnes of magnesium?
Solution
48g Mg → 238g U
24tonnes Mg → x
cross multiply to find the answer
Answer:
Limiting reagent
A limiting reagent is a reactant that is in short supply by the mole ratio and hence it finishes before the other reactants are completely reacted.
A limiting reagent is always smaller or in less quantity compared to the other reactant
A limiting reagent is found by dividing the number of moles of each reactant by its stoichiometric coefficient in balanced chemical equation.
A limiting reagent determines the extent to which the chemical reaction can proceed and the amount of products that would be formed. Once the limiting reagent is finished, the reaction stops even if the other reactants are still available in the reaction vessel.
For this reason, it is important to identify the limiting reagent before calculating the theoretical yield
In the identification of the limiting reagent
- The balanced chemical equation and the mole ratio of reactants are used
- You cannot use volumes, concentrations or masses of the reactants since these will easily mislead you.
Note An excess reagent is a reactant that remains unreacted at the end of the reaction.
Example 13
19.5g of zinc and 9.40g of sulphur were heated together
Zn(s) + S(s) → ZnS(s)
(a) Which of the two is the limiting reactant?
(b) How many moles of zinc remain unreacted?
(c) How many grams of zinc element remain unreacted?
(d) Calculate the mass of zinc sulphide formed
Solution
(a)
The limiting reagent is sulphur because it has a smaller number of moles compared to zinc.
(b)
Number of moles of Zn unreacted = 0.3mol – 0.29mol
(c)
m = n x MM
m = 0.01mol x 65g/mol
m = 0.65g of Zn remained unreacted
(d)
32g S → 97g ZnS
9.4g S → x
Answer: x = 28.5g ZnS
Gas volume (Molecular volume of gases)
Avogadro’s law
The law states that: the volume of a gas is directly proportional to the number of moles of the gas molecules present if the pressure and temperature are constant
n = number of moles [mol]
V = volume [cm3] or [dm3]
Vm = molar volume [cm3/mol] or [dm3/mol]
Room temperature and pressure (r.t.p): The volume of one mole of any gas is 24dm3 or 24000cm3 at r.t.p
Standard temperature and pressure (s.t.p): The volume of one mole of any gas is 22.4dm3 or 22400cm3 at s.t.p
Example 14
(a) Calculate the number of moles of carbon dioxide molecules present in 240cm3 of gas at r.t.p
Solution
Answer: n = 0.01 mol
(b) What volume of hydrogen measured at s.t.p is produced when 0.35g of Lithium reacts with water?
Solution
n = 0.05mol
2 mol Li → 1mol
0.05mol Li → x
n = 0.025mol
V = n x Vm
V = 0.025mol x 22.4dm3/mol
Answer: V = 0.56dm3
Relative molecular mass of gases
Example 15
The density of a gas is 0.71g/dm3 at r.t.p. What is the mass of the gas?
Solution
Mass = Density x volume
= 0.71g/dm3 x 24dm3
= 17.04g
Concentration
Concentration is the amount of solute dissolved in a unit volume of the solution.
The concentration expressed in mol/dm3 is called molarity.
M = Molarity [mol/dm3]Molarity is the number of moles of solute in one liter of solution
n = moles [mol]
V = volume [dm3]
Example 16
(a) A solution of glucose contains 0.45g of glucose in 0.075dm3 of solution. Calculate the concentration of glucose solution in g/dm3 .
Solution
Answer: 6.0g/dm3