vectors
vectors refers to the movement from one point to another. A vector quantity consists of direction and magnitude/length
« Previous Next »Deriving a vector from a graph
The graph below shows vector AB having direction and length. From the graph drawn to make up the components of a vector which is the x and y axis one must taken down the point where the vector lays on X and also on the Y axis
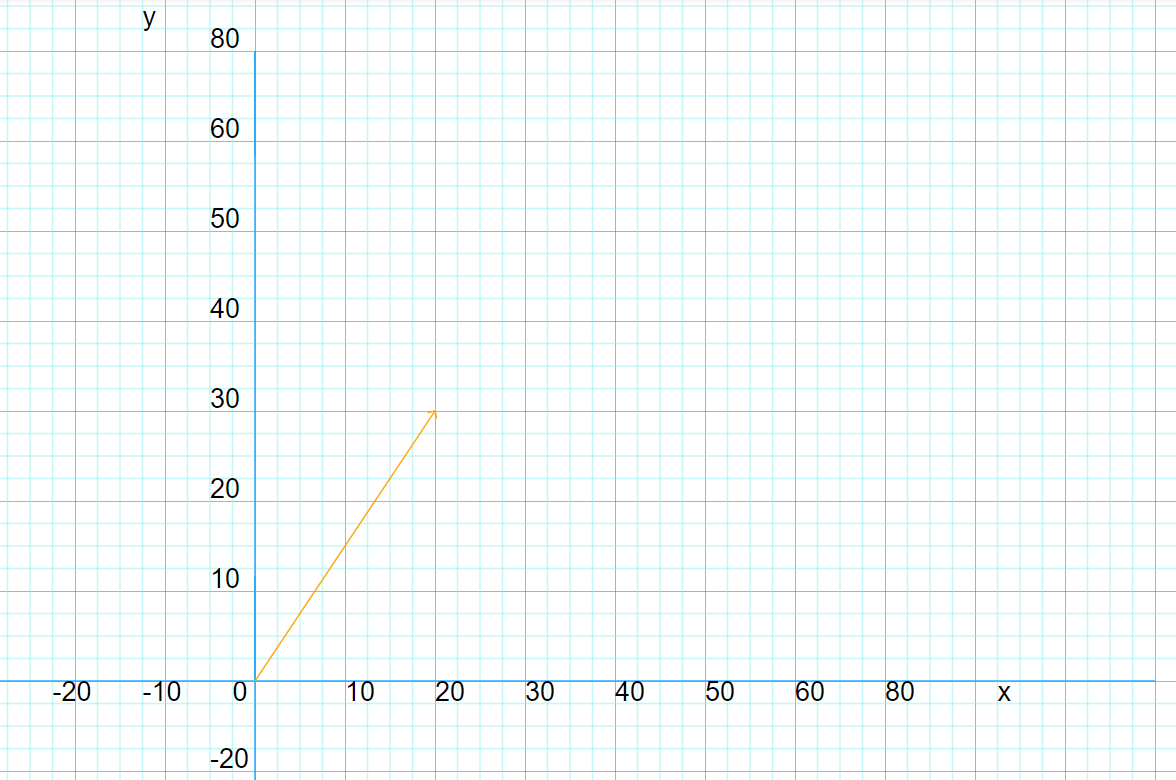
vector AB = [20, 30] or =
Points to note
A vector has both magnitude and direction but a scalar has magnitude only.
A vector may be represented by or a like symbol.
The magnitude of a column vector a = is given by |a| =
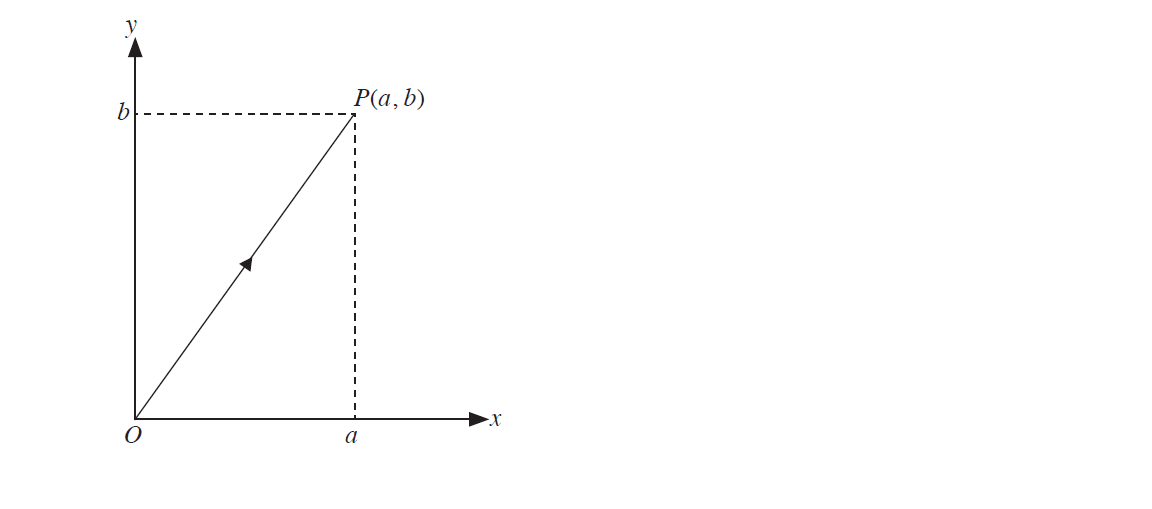
Position Vectors
If the point P has coordinates (a, b), then the position vector of P, , is written as =
Equal Vectors
Two vectors are equal when they have the same direction and magnitude.

Negative Vector
is the negative of .
is a vector having the same magnitude as but having direction opposite to that of .
We can write = and = .

Zero Vector
A vector whose magnitude is zero is called a zero vector and is denoted by 0.
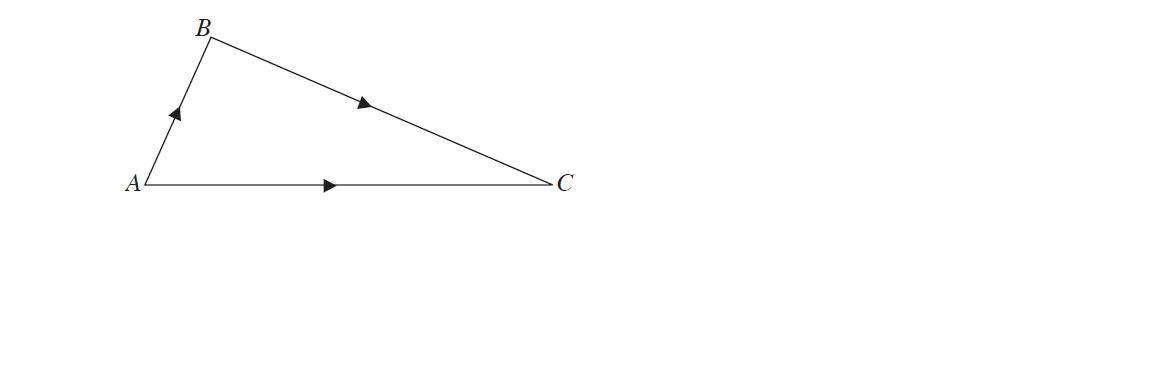
Sum and Difference of Two Vectors
The sum of two vectors, a and b, can be determined by using the Triangle Law or Parallelogram Law of Vector Addition.
Triangle law of addition:
+ =
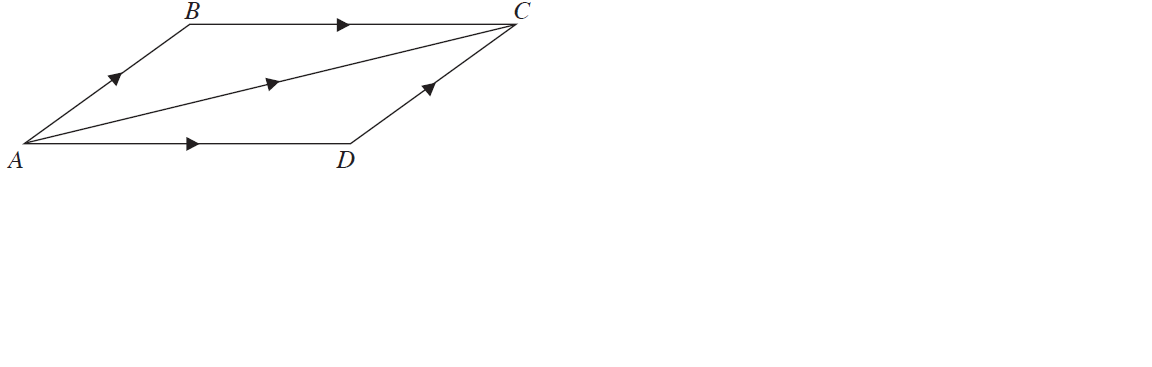
Parallelogram law of addition:
+ = + =
How to solve vectors step by step
Given that 𝒂 = ,𝒃= and 𝒄= , evaluate;
(i) a + b,
(ii) a – c,
(iii) c – b,
Solutions:
(i)
Addition of vectors
a + b
a = , b =
+
Answer: a + b =
(ii)
Substraction of vectors
a - c
-
Answer:
(iii)
c – b
-
Answer:
How to solve vectors with examples
The diagram below shows a parallelogram where AB = p and BC = q, the point E on AD is such that AE = AD
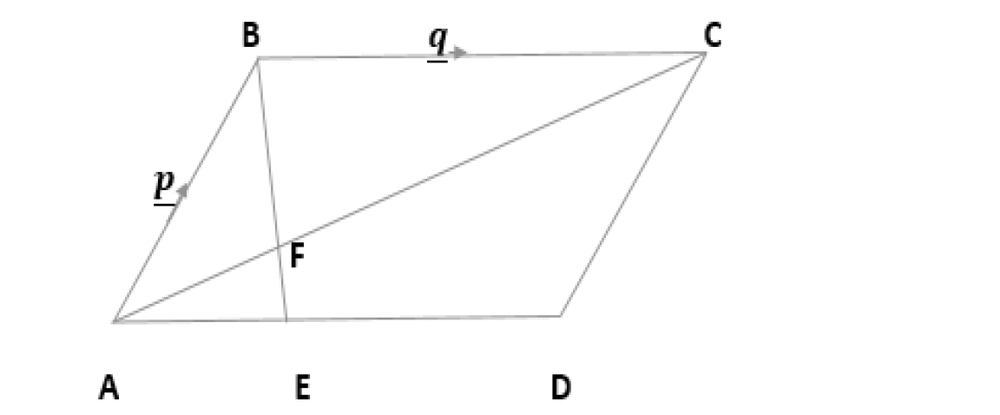
(i) Express in terms of p and/or q vectors
(a) AC
(b) AE
(c) BE
(ii) AC and BE intersect at F. Given that BF = kBE Express BF in terms of p, q and K.
(iii) Hence show that AF = (1 - k)p + 1/4kq
Solutions:
(i)
(a)
We first come up with the formula, what we want is to use to find AC
= +
substitute into the formula to find AC
= p + q
Answer: = p + q
(b)
Look at the first statement in the question, there is already a formula for AE which says, AE = AD and having in mind that the diagram above is a parallelogram then AD = BC. Given tha BC = q
AE = q
Answer: AE = q
(c)
Formula for BE is :
= +
Note that: is the negative vector of , hence = -p
substitute in the formula
= - p + q
= q - p
Answer: = q - p
(ii)
Formula to solve BF = kBE and expressing it in terms of p, q and k
substitute in the formula given that = q - p
BF = kq - p
BF = kq - kp
Answer: = kq - kp
(iii)
We have to come up with a formula to prove that AF = (1 - k)p + 1/4kq
Formula
= +
We already have = p and BF = kq - kp, hence we can just substitute
= p + kq - kp
= p - kp kq
= (1 - k)p kq
Answer: = (1 - k)p kq
hence shown
How to solve vectors
In the diagram below, Q is the midpoint of OC and OABP is a straight line with OA = AB = BP, OA = 2p and OQ = q
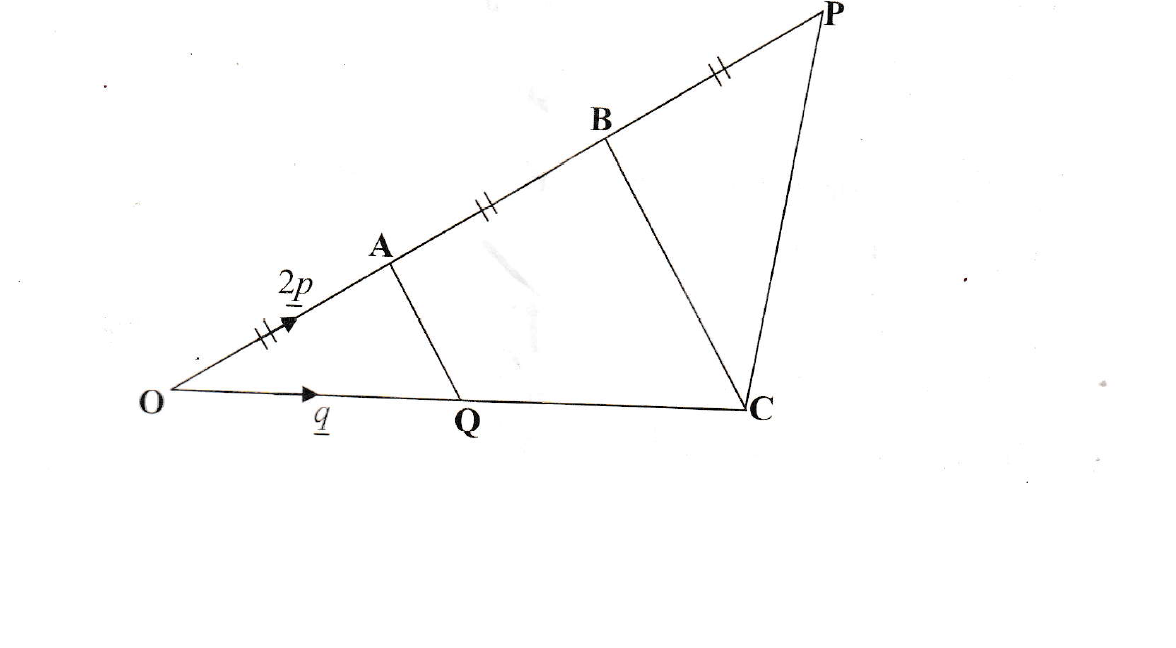
Express in terms of p and/or q
(i) OB
(ii) BC
(iii) AQ
(iv) CP
Solution:
(i)
OB =
Answer:
(ii)
Answer:
(iii)
Answer:
(iv)
Answer:
How to solve vectors with ratios
In the diagram below, OP = 2q, OQ = 4q and PX : XQ = 1 : 2
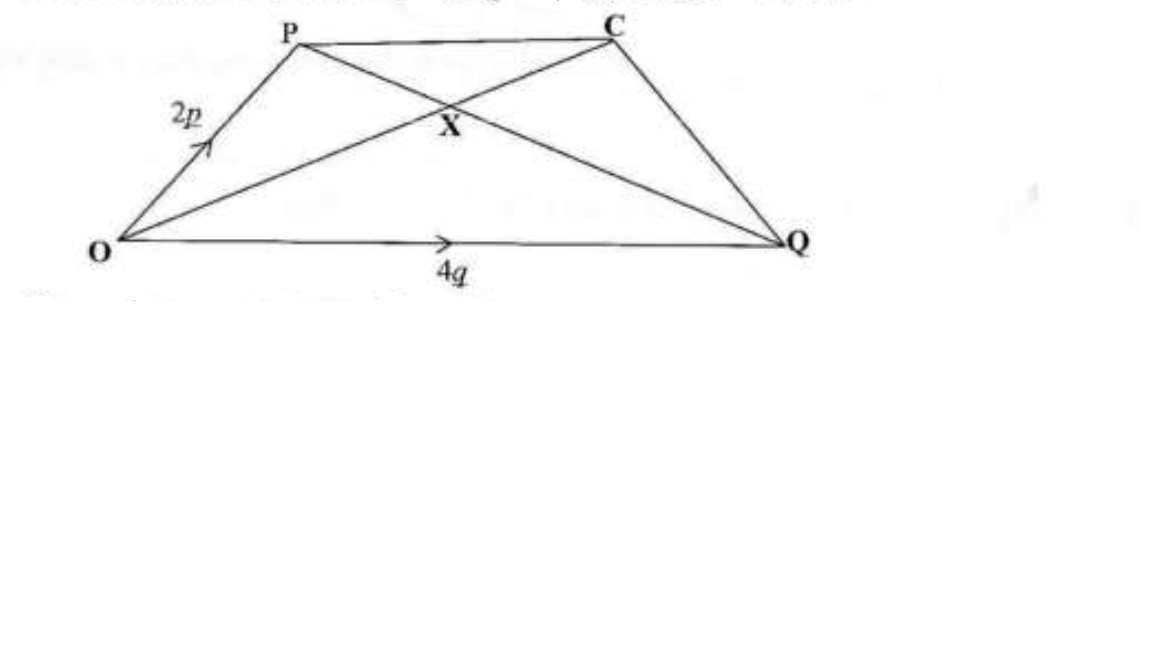
(i) Express in terms of p and/or q
(a) PQ
(b) PX
(c) OX
Solution:
a)PQ
PQ = PO + OQ
= -2p + 4q
Answer: PQ = 4q -2p
Point to note
When the vector is moving in the opposite direction it becomes negative E.G OP = 2p its opposite is PO = -2p
b)PX
PX =
=
=
Answer: PX =
c) OX
OX = OP + PX
=
=
=
=
Answer: OX =