Work, Energy and Power

Work

Work is defined as the product of the force and the distance moved in the direction of the force

The unit of work is Joule [J].

Formula for work

$W=\mathrm{Fd}$

W: Work [J]

F: Force [N]

d: distance moved in the direction of the force [m]

If a man pushes an object on the floor, he does the work on the object because the distance is in the same direction of the force.

But if a woman carries a container on her head, she does no work on the container because the distance is in the different direction of the force. (in this case perpendicular to the force)

Example

A force of 5N acts on a 3kg brick, moving it 8m horizontally from rest. Find the work done by the force.

Solution

$W=\mathrm{Fd}$

Given that

F = 5N

d = 8m

W = ?

$W=5\times 8$

Answer: $W=\mathrm{40j}$

Energy

Energy is defined as the ability to do work.

The unit of energy is Joule [J].

Potential energy

Potential energy is defined as the energy by the position or state of an object. The potential energy due to height is called gravitational potential energy.

Formula for Potential Energy

$\mathrm{PE}=\mathrm{mgh}$

PE: Potential energy [J]

m: mass [kg]

g: acceleration due to gravity [m/s2]

h: height [m]

Example

A 20kg object is raised to a height of 5m. What is its potential energy?

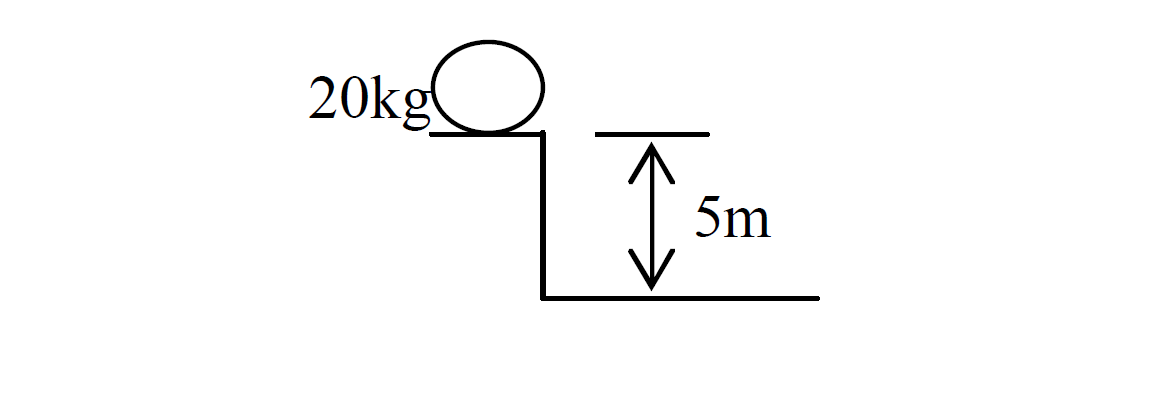
Solution

$\mathrm{PE}=\mathrm{mgh}$

m = 20kg

g = $\mathrm{10m/s}2$

h = 5m

PE = ?

$\mathrm{PE}=\mathrm{20}\times \mathrm{10}\times 5$

Answer: $\mathrm{PE}=\mathrm{1000j}$ or $\mathrm{1kj}$

Kinetic energy

Kinetic energy is defined as the energy due to the motion of an object.

Formula for Kinetic energy

$\mathrm{KE}=\frac{1}{2}{\mathrm{mv}}^2$

KE: Kinetic energy [J]

m: mass [kg]

v: velocity [m/s]

Example

A 2kg stone is thrown with a velocity of 5m/s. What is its kinetic energy?

Solution

$\mathrm{KE}=\frac{1}{2}{\mathrm{mv}}^2$

Given that

m: 2kg

v: 5m/s

KE: ?

$\mathrm{KE}=\frac{1}{2}{\mathrm{2(5)}}^2$

$\mathrm{KE}=\frac{1}{2}\mathrm{2(25)}$

$\mathrm{KE}=\frac{1}{2}\mathrm{50}$

$\mathrm{KE}=\mathrm{25j}$

Conservation of energy

Law Energy can be changed from one form to another, but cannot be created or destroyed.

Example

If a ball falls freely from a certain point, how does the energy change?

Solution

1. Before a ball is released, its potential energy is 1000J and the kinetic energy is 0J because it doesn’t move.

2. At the midpoint of its journery, the potential energy drops to 500J but the kinetic energy increses to 500J. Total energy is still 1000J.

3. Just before hitting the ground, the potential energy becomes 0 J but the kinetic energy increases to 1000J. There is no change in the total energy throughout itsfalling

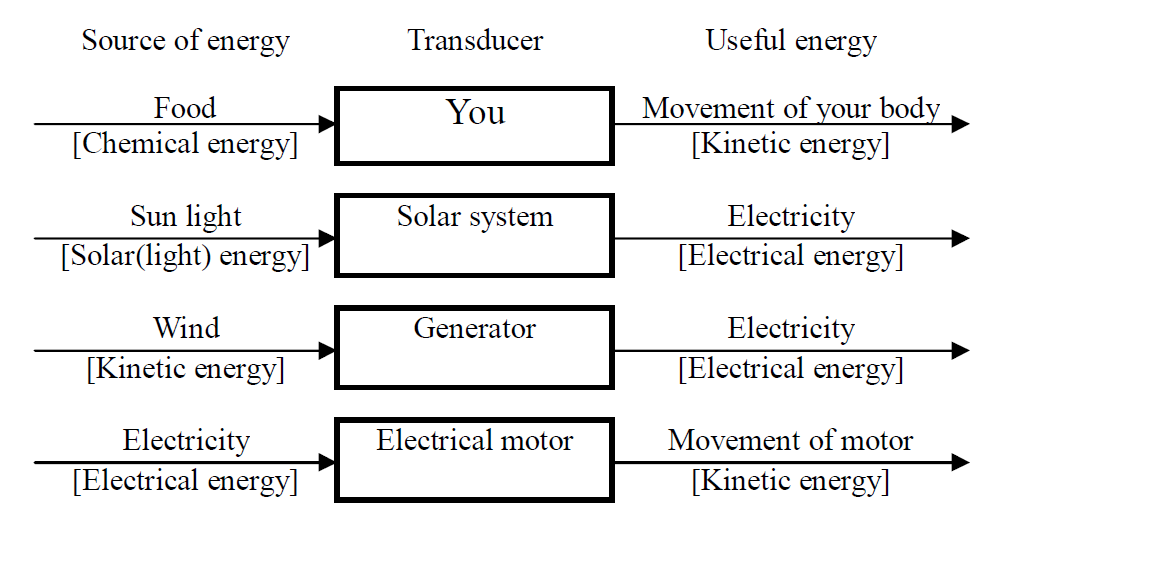
Use of energy (Source, Transducer, Use)

When energy is used for our life,first energy comes from energy sources, and the energy forms are changed by a transducer. Then useful energy is provided. The diagrams below show some examples of sources of energy, transducers and useful energy provieded.

Environmental effect

If sources of energy are used in our life, it may affect on the environment. The followings show some cases of effect to enviroment. We must prevent such kind of bad influence.

Case 1 Effect of a Car

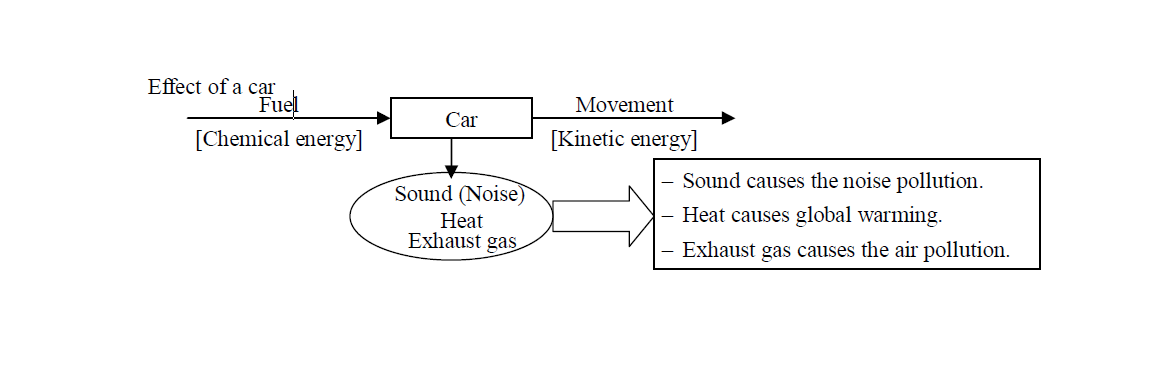
Case 2 Effect of a hydraulic Plant

Hydrauric plants are clearn. It doesn’t cause any pollution. However it may changes natural ecosystem. When the dam is built, very large space is needed. Many trees are cut. It is a deforestration. And also many living things (animals and insects) lose their living places.

Case 3 Effect (risk) of an atomic Plant

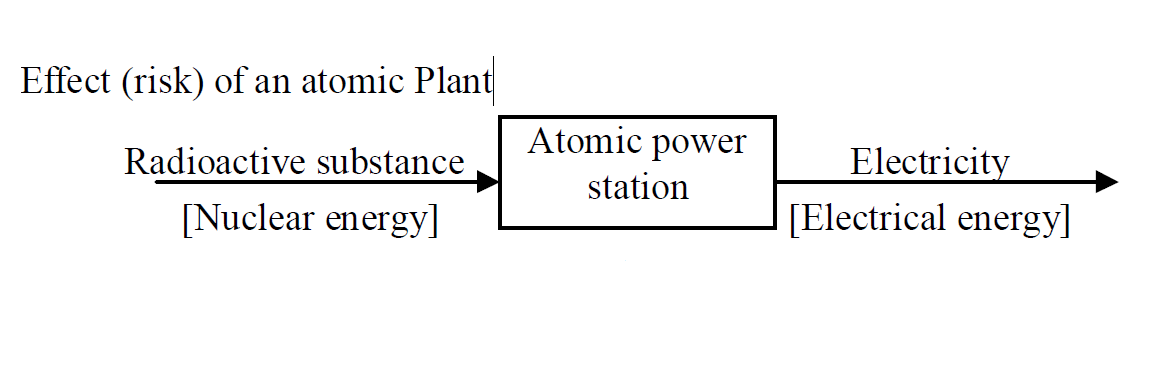
If an atomic power station is damaged, the radiation leaks. It brakes cells or gene of living things. As a result, it causes some diseases such as cancer.

Power

Power is defined as the rate of doing work.

Formula for Power

$P=\frac{W}{\mathrm{t}}$ or $P=\frac{E}{\mathrm{t}}$

Example

A crane can lift 200kg to a height of 100m in 20s. What is the useful power of the crane?

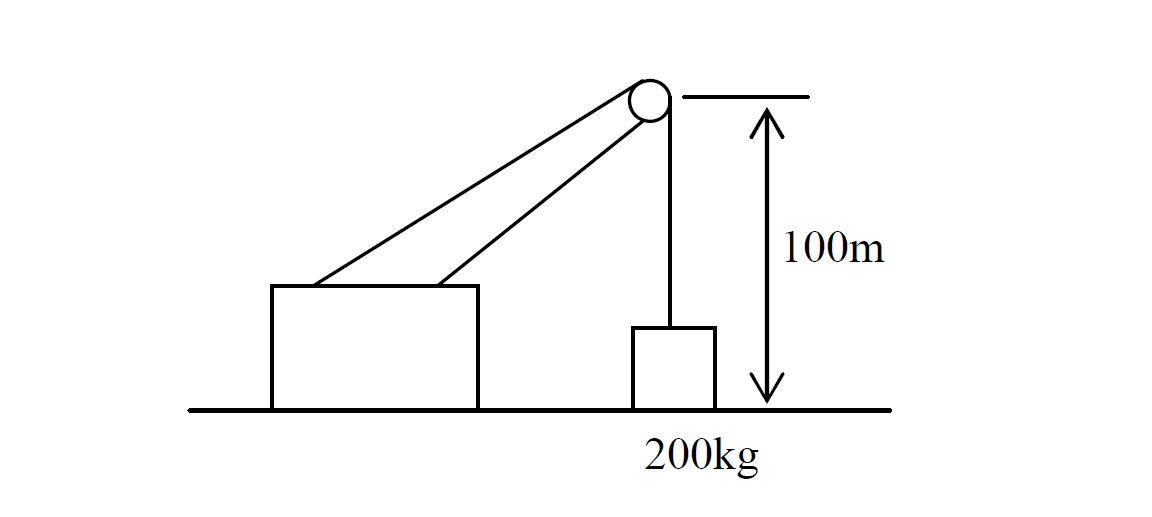
Solution

Steps to take

1. Find the weight.

2. Find the work done.

3. Find the power.

Find Weight

$W=\mathrm{mg}$

Given that

W = ?

m = 200kg

g = $\mathrm{10m/s}2$

$W=200\times \mathrm{10}$

$W=\mathrm{2000N}$

Find Work done

$\mathrm{Work}=\mathrm{Fd}$

Given that

Work= ?

F = Weight = 2000N

d = 100m

$\mathrm{Work}=2000\times \mathrm{100}$

$\mathrm{Work}=\mathrm{200,000j}$

Find Power

$P=\frac{W}{\mathrm{t}}$

Given that

P = ?

W = 200, 000j

t = 20s

$P=\frac{\mathrm{200000}}{20}$

Answer: $P=\mathrm{10,000W}$ or $P=\mathrm{10kW}$