Moment of a force

Moment of a force about a pivot is defined as the product of the force and the perpendicular distance of its line of action from pivot.

Moment of a force about a pivot is defined as the product of the force and the perpendicular distance of its line of action from pivot.

Formula for moment

$M=\mathrm{Fd}$

M: Moment [Nm]

F: Force [N]

d: perpendicular distance [m]

- Perpendicular distance must be a distance from the pivot to the force.

- Perpendicular distance must be at right angle to the force.

Example

Calculate the moment of the force at the pivot.

$M=\mathrm{Fd}$

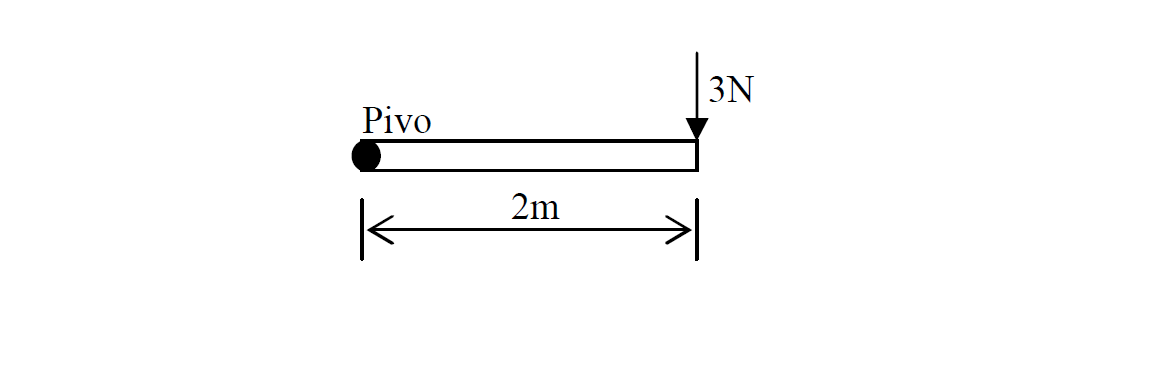
Given that

F = 3N

d = 2m

$M=\mathrm{3(2)}$

$M=\mathrm{6Nm}$

Principal of moment

Law For a body to be in equilibrium (balanced), the sum of clockwise moments about any point is equal to the sum of anticlockwise moments about the same point.

Formula

Total clockwise moment = Total anticlockwise moment

$\mathrm{F1\; d1}=\mathrm{F2\; d2}$

Conclusion: If a body is balanced, then the total clockwise moment is equal to the total anticlockwise moment.

Example 1

Calculate the force F if it is balance

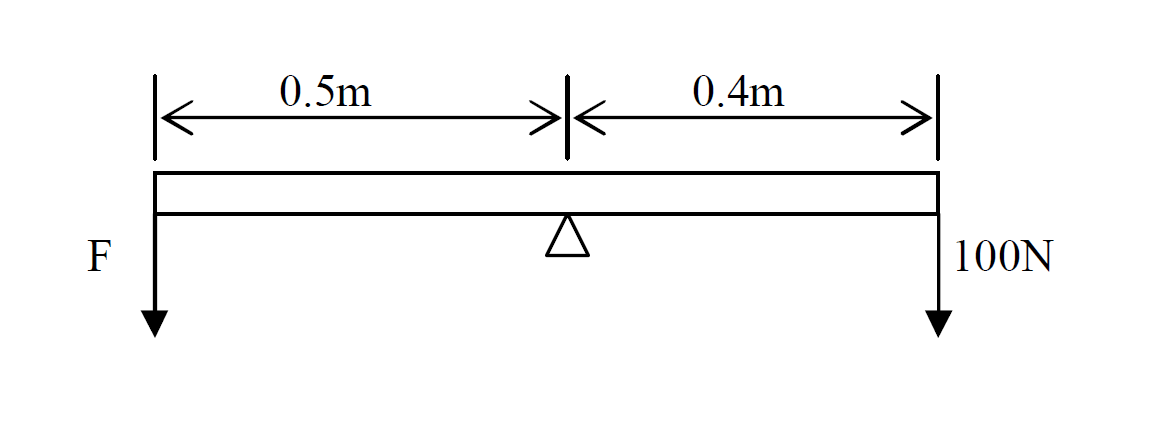
Solution

$\mathrm{F1\; d1}=\mathrm{F2\; d2}$

Given that

F1 = F ?

d1 = 0.5m

F2 = 100N

d2 = 0.4m

$F\times 0.5=\mathrm{100}\times 0.4$

$\mathrm{F0.5}=\mathrm{40}$

$\frac{\mathrm{F0.5}}{0.5}=\frac{\mathrm{40}}{0.5}$

Answer: $\mathrm{F}=\mathrm{80N}$

Example 2

Calculate the distance d if it is balanced.

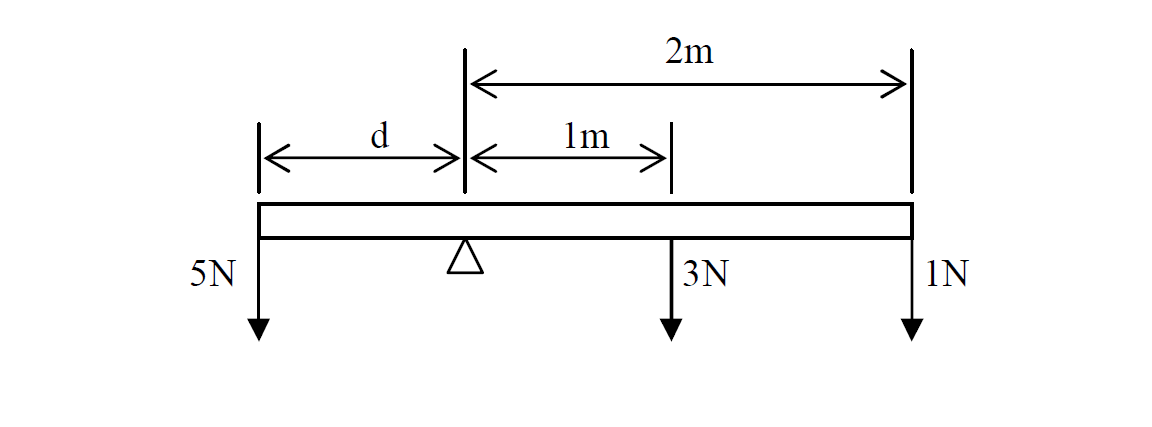
Solution

$\mathrm{F1\; d1}=\mathrm{F2\; d2}$

Given that

F1 = 5N

d1 = d ?

F2 = 3N, 1N

d2 = 1m , 2m

Find the two moments on the right hand side of the moment and then add those moments

$M=\mathrm{Fd}$

$M=3\times 1$ = 3Nm

$M=1\times 2$ = 2Nm

Therefore moment on the right hand side is: $\mathrm{3Nm}+\mathrm{2Nm}=\mathrm{5Nm}$

Merge the moments to find the distance d

$\mathrm{F1\; d1}=\mathrm{F2\; d2}$

$\mathrm{5\; d}=5$

$\frac{\mathrm{5\; d}}{5}=\frac{5}{5}$

Answer: $d=\mathrm{1m}$